Bean Machine Graph Inference
What is Bean Machine Graph Inference?
Bean Machine Graph (BMG) inference is an experimental implementation under active development of inference methods intended for use on a restricted set of models. It uses a compiler (internally referred to as Beanstalk) which is automatically executed, without user intervention.
BMG inference is still used on models defined in Python as usual, but relies on a C++ runtime and therefore bypasses Python overhead during inference. Moreover, it is designed specifically to gain significant performance improvements for inference in models with the following properties:
- These models are unvectorized, that is, their stochastic quantities are tensors which contain exactly one value.
- They are static, that is, their corresponding graph is the same regardless of the values of random variables’ values. To get a better idea of what a model's graph is and when it is static, see section Model graphs (static and dynamic) below.
Examples
The tutorials currently working with BMG inference are:
- Linear regression Open in GitHub • Run in Google Colab;
- Neal's funnel Open in GitHub • Run in Google Colab.
For the above three models, the BMG version of Newtonian Monte Carlo (NMC) inference reduces runtime to generate samples of size 10K for the posterior distribution by anywhere between 80 and 250 times depending on the model.
Model Restrictions
In this release, models accepted by BMG inference have the following restrictions:
- With some exceptions, all tensor quantities manipulated by the model must be single-valued. There is some limited support for one- and two-dimensional tensors.
- They represent static probabilistic graphs
@random_variablefunctions must return a univariateBernoulli,Beta,Binomial,Categorical,Chi2,Dirichlet,Gamma,HalfCauchy,HalfNormal,Normal,StudentTorUniform(0., 1.)distribution.- Tensor operators on stochastic values are limited to
add(),div(),exp(),expm1(),item(),log(),logsumexp(),mul(),neg(),pow(),sigmoid()andsub(). - Python operators on stochastic values in
@random_variableor@functionalfunctions are limited to+,-,*,/, and**operators. Matrix multiplication and comparisons are not yet supported. - Support for the
[]indexing operation is limited. - Support for "destructuring" assignments such as
x, y = zwherezis a stochastic quantity is limited. - All
@random_variableand@functionalfunctions in the model and every function called by them must be "pure". That is, the value returned must be logically identical every time the function is called with the same arguments, and the function must not modify any externally-observable state. - Models must not mutate existing tensors "in place"; always create new values rather than mutating existing tensors.
- Conditions of
whilestatements,ifstatements, andifexpressions must not be stochastic.
Using BMG Inference
To use Bean Machine Graph inference on a Bean Machine model, first import the inference engine with the following command: from beanmachine.ppl.inference.bmg_inference import BMGInference.
The BMGInference class provides the following methods to perform inference and inspect the graph analysis:
BMGInference().infer(queries, observations, num_samples, num_chains)- Computes the static dependency graph and executes inference using Bean Machine Graph; returns a dictionary of samples for the queried variables. In the current release only Newtonian Monte Carlo (NMC) is supported when running inference withBMGInference.BMGInference().to_graphviz(queries, observations)- Returns a graphviz figure representing the static graph of the model.BMGInference().to_dot(queries, observations)- Returns the DOT source code of the graphviz static graph.
We have a number of informative error messages that may be emitted that should help you to debug any issues with using BMG inference, but if you happen to (rarely, we hope) encounter any crashes or fails with an unclear error message, please file an issue at https://github.com/facebookresearch/beanmachine/issues.
Model graphs (static and dynamic)
The graph of a model is defined by nodes representing the mathematical objects in the model (constants, random variables, results of operations, and distributions), and edges representing dependencies in the model. If a quantity node N depends directly on nodes M1, M2, ..., Mk, then there is an edge from each Mi to N.
For an example, consider the Bean Machine model specified in Python below and its corresponding graph.
@random_variable
def a():
return Normal(0, 1.)
@random_variable
def b():
return Normal(a() + 5, 1.)
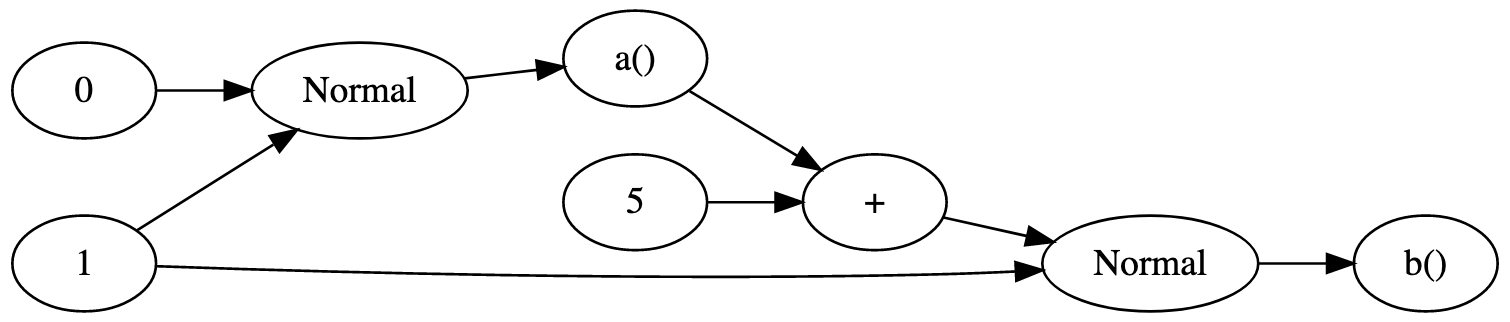
This graph is static because the dependencies are the same regardless of the values involved (for example, a() is always a sample of the Normal(0,1) distribution regardless of its value).
A graph is not static (that is, dynamic) if dependencies do change according to random variable values. Consider the following model:
@random_variable
def a(i):
return Normal(i, 1.)
@random_variable
def index():
return Poisson(0.3)
@random_variable
def b():
return Normal(a(index()) + 5, 1.)
This model does not have a static graph because the expression a(index()) + 5 in the last line will depend on different nodes a(index()), depending on the value of index().